Verlet Integration: Rendering The Rope

Source: ScreenRant

Verlet integration is a numerical method originating from molecular physics that calculates particle trajectories. This method is also widely used in computer graphics and physics simulation.

I used this method to simulate rope physics. I highly recommend checking it out here before reading this article. I implemented its physics and collision detection.

Verlet Integration: Simulating Rope Physics in Unity

Currently, we can only see our rope in the scene view using gizmos, in the game view we see nothing. In this article, we will procedurally generate a 3D mesh for our rope so we can actually see it in our game.

The rope can only be seen in the Scene view using gizmos

How are we going to do it?

We divide our rope into various segments divided by our verlet nodes. We see each segment as a cylinder-like shape with n sides. We put our vertices around the verlet nodes in the form of an equilateral polygon. This polygon is on a plane consisting of the verlet node and the vector towards the next verlet node as the normal of the plane.

Then, we form our triangles, pass the data to the rope’s mesh filter, update whatever we want and that’s it.

Finding the vertices

In order to make an equilateral polygon as described above, we need to use some linear algebra and analytical geometry knowledge. We need to define a circle on a plane in 3D space and find the vertices on it.

First, We find a circle with a radius equal to our rope radius and then we have to parameterize it so we can find points on it giving an angle. To do this, we need to find two perpendicular vectors lying on a 3D plane called u and v. This plane has our verlet node on it and its normal vector is the vector starting from the current node and pointing to the next one.

To find these vectors we need to find another vector. It can be anything but it shouldn’t be parallel with n. Let’s take Vector3.forward for instance and call it v1. Now we can calculate u.

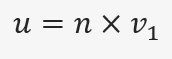
To calculate v, we normalize u, and calculate its cross product with the normal vector.

Now we can make our parameterized circle equation. The equation will be as follows.

This equation describes a circle on the plane we want with the radius r, with its center at p. It takes an angle as the input and gives us a point on the circle corresponding to that angle.

Now we can write the code for finding the vertices for our mesh. Unity mesh filter gets the vertices as an array of Vector3s.

private void ComputeVertices(VerletNode[] nodes, float radius)
{
    var angle = (360f / m_RopeSegmentSides) * Mathf.Deg2Rad;

    for (int i = 0; i < m_Vertices.Length; i++)
    {
        var nodeindex = i / m_RopeSegmentSides;
        var sign = nodeindex == nodes.Length - 1 ? -1 : 1;
        Debug.Log($"Node Index: {nodeindex}, Vert Index: {i} , {m_Vertices[i]}");
            
        var currNodePosition = nodes[nodeindex].Position;
        var normalOfPlane =
            (sign * nodes[nodeindex].Position + -sign * nodes[nodeindex + (nodeindex == nodes.Length - 1 ? -1 : 1)].Position)
            .normalized;

        var u = Vector3.Cross(normalOfPlane, Vector3.forward).normalized;
        var v = Vector3.Cross(u, normalOfPlane).normalized;

        m_Vertices[i] = currNodePosition + radius * (float)Math.Cos(angle * (i % m_RopeSegmentSides)) * u +
                        radius * (float)Math.Sin(angle * (i % m_RopeSegmentSides)) * v;
    }
}

The sign variable is to calculate the normal vector when we reach the last node of the rope. We have to use the vector towards the previous node as the normal of the plane since there is no next node.

We need to turn the coordinates of the vertices local to the rope itself and then we can pass it to the mesh filter.

Vertices of a rope with 5 sides, shown with gizmos

Building the triangles

Now that we have the vertices, we can find the triangles. We are going to make the triangles look similar to the default cylinder.

Triangles of a default cylinder

The way mesh filter processes triangles is different than vertices. It gets an array of integers. Each number in this array is the index of a certain element in the vertices array. Each 3 numbers in the triangles array refer to the vertices building a single triangle.

The catch is that we need to insert these indexes in clockwise order. If we don’t do so, the triangle will not be visible from the side we want, but from the other side.

We will take a window of two vertices each time, moving on the vertices around a node of the rope. then we will make triangles using the vertices around the next node and in front of the current vertices.

private void ComputeTriangles()
{
    var tn = 0;

    for (int i = 0; i < m_Vertices.Length - m_RopeSegmentSides; i++)
    {
        var nexti = (i + 1) % m_RopeSegmentSides == 0 ? i - m_RopeSegmentSides + 1 : i + 1;

        m_Triangles[tn] = i;
        m_Triangles[tn + 1] = nexti + m_RopeSegmentSides;
        m_Triangles[tn + 2] = i + m_RopeSegmentSides;

        m_Triangles[tn + 3] = i;
        m_Triangles[tn + 4] = nexti;
        m_Triangles[tn + 5] = nexti + m_RopeSegmentSides;

        tn += 6;
    }
}

the nexti variable is because when we reach the last vertex around a node, the next vertex should be the first one, i.e. to loop around the rope.

Triangles and vertices of a rope with 5 sides, shown using gizmos

Updating the mesh filter

Now all we need to do is pass the data we generated to the mesh filter. We make the position of the vertices local to the position of the rope. Then, clear the mesh of the mesh filter, pass the vertices and triangles array, and recalculate bounds and normals.

private void SetupMeshFilter()
{
    for (int i = 0; i < m_Vertices.Length; i++)
    {
        m_Vertices[i] -= transform.position;
    }
        
    m_RopeMesh.Clear();
    m_RopeMesh.vertices = m_Vertices;
    m_RopeMesh.triangles = m_Triangles;

    m_MeshFilter.mesh = m_RopeMesh;
    m_MeshFilter.mesh.RecalculateBounds();
    m_MeshFilter.mesh.RecalculateNormals();
}

Then we make a material with the standard shader and give it the color we want.

Behold! A rope that we can see!

After implementing rope physics and collision detection and resolution for it, we rendered this rope by procedurally generating a cylinder-like shape for it. We used knowledge from linear algebra and analytical geometry to generate vertices, made triangles using them, and rendered them by interacting with the mesh filter component.

you can find the source code for this project here:

GitHub - alirezaft/UnityVerletRope: Implementation of rope physics in Unity using Verlet…

As you can see there are a lot that can be improved. A shader can let us add a nicer texture to it, and the mesh generation is on the CPU side which makes it slow and computationally expensive. There’s gotta be a way to hand it to the GPU side. I’d be happy to know how you would do it in the comment section, so let me know!