Verlet Integration: Simulating Rope Physics in Unity

One of the most important parts of game development is simulating physics, things like collision, applying forces, and more advanced things like deforming objects, destructions, etc. One of the problems in physics simulation is simulating rope physics accurately and efficiently.
In this article, we will implement rope physics in Unity using Verlet integration. We will also make a simple renderer for our rope to render a cylinder-like shape for our rope in future.
What is Verlet Integration?
Verlet integration is a numerical method for integrating Newton’s equations of motion. It is mostly used in molecular dynamics to calculate the trajectories of particles.
But it’s not the only place Verlet integration is used. It is widely used in computer graphics and video games to simulate several physical phenomena and visual effects like particle systems, i.g. particles systems, ragdolls, ropes, rigid bodies, etc.
Verlet integration works using a timestep-based approach. Instead of continuous time, it does its calculations in a frame-by-frame manner. In each timestep, it calculates the next position of the particle using its current position, previous position, and the current acceleration of the particle.
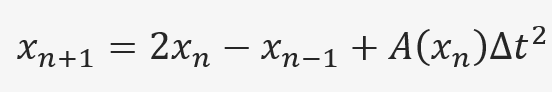
xn+1 is the next position.
xn is the current position.
xn-1 is the previous position.
A(xn) is the acceleration of the particle in the current position.
and delta t is the difference between time steps.
(I hope medium adds support for math equations one day.)
For particles without any constraints, this equation alone works fine. But if you need to maintain a certain distance between particles, you need to apply constraints using the following method.
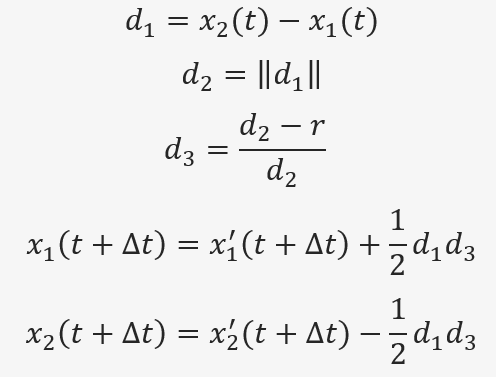
This formula takes two particles and moves them closer together each time step.
x’ is the unadjusted position without constraints applied and x is the adjusted position.
delta t is the length of our timestep.
This method has many advantages. It is straightforward and easy to understand, and it needs very little space for storing necessary variables. But it has one downside: Its accuracy is not that high, but it’s enough for simulating physics in video games.
How to Use This to Simulate a Rope?
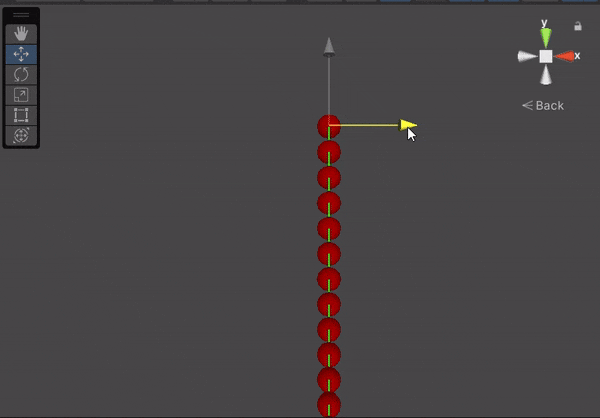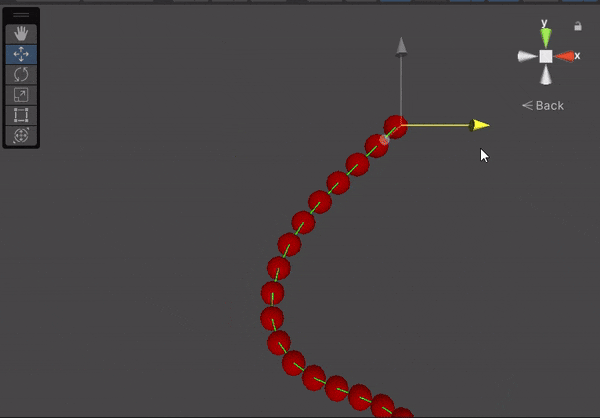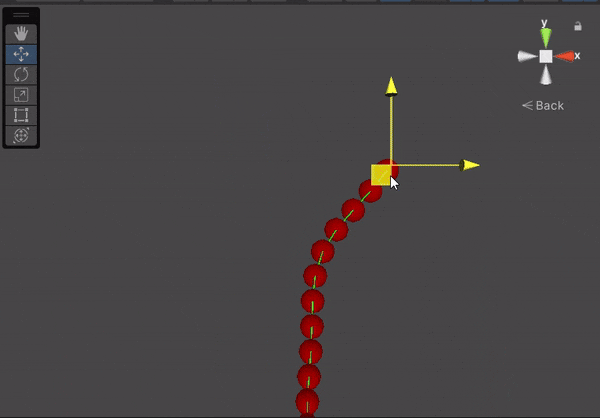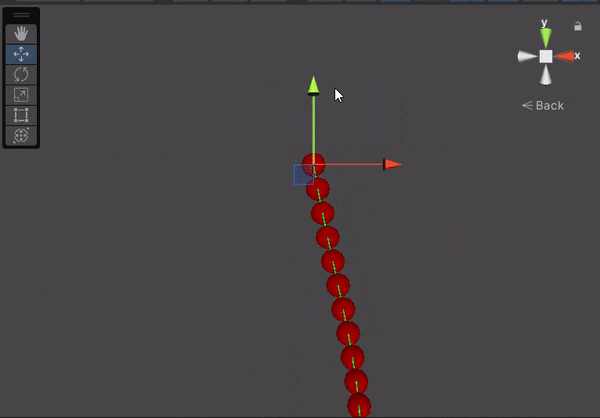
The idea is to consider our rope as a bunch of particles or nodes connected back to back, like a chain. We will apply Verlet integration to each node to calculate their position. Then, since our rope doesn’t stretch or shrink, we need to apply constraints to them to maintain a constant distance between the nodes. We will also need to implement collision resolution and render our rope in the 3D space.
Basic Implementation
First, we need to have a structure to represent our nodes. All we need to store is the current and previous positions.
public struct VerletNode
{
public Vector3 Position;
public Vector3 PrevoiusPosition;
}Now we can consider our rope as an array of VerletNode .
Then we need to implement the formulas of the Verlet integration. No need to modify anything, we just turn the formulas into code.
private void CalculateNewPositions(){ //Verlet Integration
for (int i = 0; i < m_VerletNodes.Length; i++)
{
var currNode = m_VerletNodes[i];
var newPreviousPosition = currNode.Position;
m_VerletNodes[i].Position = (2 * currNode.Position) - currNode.PrevoiusPosition +
(m_Gravity * (float)Math.Pow(Time.fixedDeltaTime, 2));
m_VerletNodes[i].PreviousPosition = newPreviousPosition;
}
}private void FixNodeDistances() //Applying constraints
{
m_VerletNodes[0].Position = transform.position;
for (int i = 0; i < m_VerletNodes.Length - 1; i++)
{
var n1 = m_VerletNodes[i];
var n2 = m_VerletNodes[i + 1];
var d1 = n1.Position - n2.Position;
var d2 = d1.magnitude;
var d3 = (d2 - m_DistanceBetweenNodes) / d2;
Debug.Log("d1: " + d1 + ", d2: " + d2 + ", d3: " + d3);
m_VerletNodes[i].Position -= (d1 * (0.5f * d3));
m_VerletNodes[i + 1].Position += (d1 * (0.5f * d3));
}
}We call two methods inside FixedUpdate , but there’s a catch. We need to apply the constraints several times in each time step, because each time we apply the constraint it brings the nodes a little closer to each other, which results in the elasticity of our rope. The more iterations of applying constraints, the stiffer our rope gets.
private void FixedUpdate()
{
CalculateNewPositions(); //Verlet simulation
for (int i = 0; i < m_ConstraintIterationCount; i++)
{
FixNodeDistances(); //Applying constraints
}
}
Implementing Collision Resolution
Although we have a rope that reacts properly to movement, It’s only a good rope implementation if it’s the only thing in the world, because it can’t handle collision. If you move this rope to any rigid body, it will pass through them.
Since we have implemented everything from scratch, we need to implement collision detection and resolution ourselves. The plan is to find the collision point, and put the colliding node on the surface, with a distance as far as the radius of the rope.
private void ResolveCollision(VerletNode node)
{
var colliders = Physics.OverlapSphere(node.Position, m_RopeRadius);
foreach (var col in colliders)
{
if (col.isTrigger) continue;
Vector3 closestPoint = col.ClosestPoint(node.Position);
float distance = Vector3.Distance(node.Position, closestPoint);
if (distance < m_RopeRadius)
{
Vector3 penetrationNormal = (node.Position - closestPoint).normalized;
float penetrationDepth = m_RopeRadius - distance;
node.Position += penetrationNormal * penetrationDepth * 1.01f;
}
}
}This code will also handle the case when the rope is resting on a surface and prevent it from penetrating the other object. But that’s not all we have to do with collision.
The main challenge is a problem called “Tunneling”. It happens when the frame in which the collision happens is dropped and the objects go through each other. This mostly happens when one of the objects is moving fast or the frame rate is too low.
In order to solve this problem, we need to do two things: 1) Divide Fixed Delta Time into substeps to increase the number of simulation frames of our rope and 2) Do sweep collision detection.
Dividing Time Steps into Substeps
By increasing the number of frames our simulation has in a time unit, we can reach a more accurate simulation that can handle faster speeds much better.
Doing such is easy. We just need to make the time steps smaller and run the Verlet integration several times in each fixed update. We pass the new time step to the CalculateNewPositions(float deltaTime) so the integration runs with the correct time step.
private void FixedUpdate()
{
for (int step = 0; step < m_SubSteps; step++)
{
CalculateNewPositions(Time.fixedDeltaTime / m_SubSteps);
for (int i = 0; i < m_ConstraintIterationCount; i++)
{
FixNodeDistances();
if (i % 2 == 0)
ApplyCollision();
}
}
}Implementing Sweep Collision Detection
The core idea behind sweep collision detection is to cast the shape of the object along the path of the object and check for imminent collisions ahead. This is one of the key parts of Continuous Physics Simulation.
To do this we use Unity’s SphereCast . Then using the hit point of the sphere cast and its normal vector, we can find the position of the node in case of a collision. We check for collisions before setting the new position as the node’s actual position. After these changes, our new method will look like this.
private void CalculateNewPositions(float deltaTime)
{
for (int i = 0; i < m_VerletNodes.Length; i++)
{
var currNode = m_VerletNodes[i];
var newPreviousPosition = currNode.Position;
var newPosition = (2 * currNode.Position) - currNode.PrevoiusPosition + gravityStep;
Vector3 direction = newPosition - currNode.Position;
float distance = direction.magnitude;
direction.Normalize();
if (Physics.SphereCast(currNode.Position, m_RopeRadius, direction, out RaycastHit hit, distance))
{
newPosition = hit.point + hit.normal * m_RopeRadius;
}
m_VerletNodes[i].PrevoiusPosition = newPreviousPosition;
m_VerletNodes[i].Position = newPosition;
}
}And this is it, a rope physics simulation in Unity!
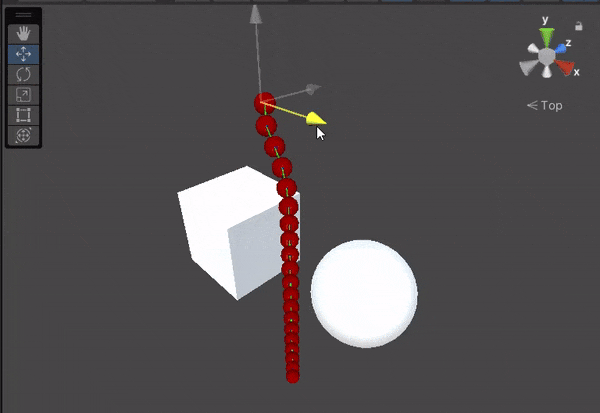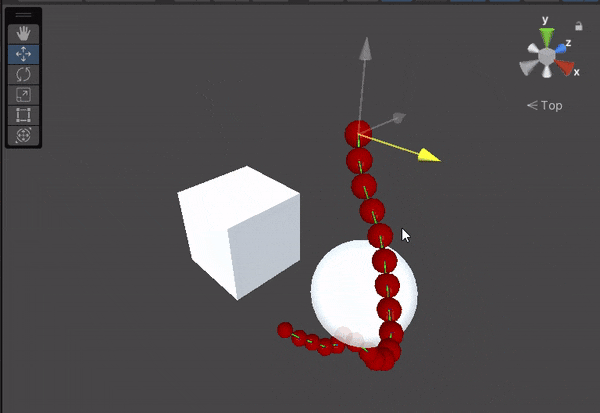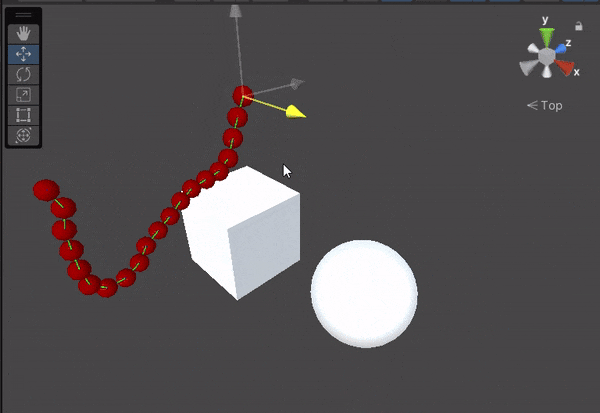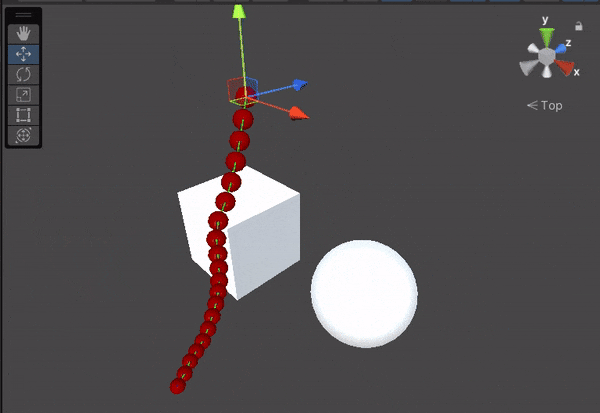
There’s just one more thing left: Rendering the rope. Our rope is still invisible in the game scene. But this article is already so long so, I will write about it soon in my next article.
Limitations
In this implementation, the rope can’t collide with itself. The rope doesn’t receive outside forces and the only force it receives is the force of gravity. It’s also computationally relatively heavy and there definitely are some optimizations to do.
Simulating physics has always been an important part of video games. in this article, we implemented rope physics in unity using Verlet integration, a method originating from molecular physics. We also implemented collision detection and resolution. you can find the github repo containing this project here.
Don’t forget to follow me to see how we will render this rope and give it a 3D mesh so we can see it in our game.
Don’t forget to check out my Boids algorithm implementation, a cool and simple algorithm that imitates the flocking behavior of birds.
What do you think about this implementation? How can we improve its performance? Are there any more features to add to it? Let me know in the comments!

